本文为原创,可在署名“胡嘉佳 曹一梅”和转自“昆明市水利学会”的前提下转载,否则视为侵权!
基于正交经验函数的云南昆明地区年季降水量空间演变特征分析
1 前言
降水空间变化有助于区域旱涝特征分析,是旱涝分析的重要数据基础[1]。近些年来,对于区域降水时空变化特征的研究有许多[2]-[8],这其中既有数理统计学方法[9]-[10],也有趋势诊断分析方法[11]-[12],但是针对其空间变化特征的研究还较少,正交经验函数也称作为EOF函数,近些年来在变量空间变化特征应用较为成熟[13]-[15],该方法结合方差分析原理,对变量空间变化的特征进行空间解译,全方位诠释变量空间变化的特性。但是在区域降水空间变化特性研究还较少,特别是在云南地区还未得到相关应用,昆明地区属于低纬度热带地区,一年四季如春,降水量充沛,但有时也较容易出现旱情,当前,在气候变化情形下,对区域旱涝变化特征有利于昆明地区的水资源优化配置。为此本文结合正交经验函数,以昆明某区域为研究范例,对该区域年季降水时空变化特征进行分析,成果对于研究昆明地区旱涝演变具有重要的参考价值。
2 正交经验函数原理
正交经验函数又称作为EOF函数,其降水空间变化分析的原理在于将降水站点数据通过内插方式得到全域降水分布,并进行标准化处理,处理后形成一个标准的降水矢量变化矩阵,矩阵方程为:

在方程中C表示为降雨矩阵数据(mm);M表示为内插数据点(个);N表示为观测雨量站点数目(个)。在矩阵确定的基础上,结合各个向量之间的方差值,计算方程为:

在方程中R表示为变量方差;T表示为方差向量个数(个)。在方差计算基础上,计算各特征雨量点的特征根和特征向量,计算方程为:

其中在方程中ΛN×N的计算方程为:

在方程中ΛN×N表示为特征向量根;λ表示为特征根。每个特征向量对应一个特征根,这就是正交函数,对其空间变化特征分析函数为:

在方程中α表示为正交经验函数的求解系数;f(z)表示为正交经验求解函数值。结合最小二乘方法原理计算各变化矩阵对应的方程求解,计算方程为:

在方程中A表示为各阶数对应的正交函数求解值;ΔC表示为计算点之间的特征分析值。
3 昆明地区降水量时空变化特征分析3.1 昆明地区降水概况
本文以云南昆明某地区为研究范例,昆明地区属于典型的低纬度温带区域,多年平均降水量约为900mm,年季降水量具有明显的变化特征,从1970年~2018年降水统计其年降水量呈现较为明显的递减变幅,除冬季外,其他季节降水也呈现减少变化,冬季降水呈现略增多变化,86%的降水主要集中在夏季和秋季,主汛期降水占全年降水的50%~60%之间,春季和冬季降水量偏少,占全年降水量的20%左右,且由于降水量的偏少,在春季出现干旱的频率达到75%以上。降水空间分布十分不均匀,东南部、南部降水量总体低于800mm,西部山区、东部降水量偏多,总体高于1000mm。
3.2 年降水正交经验函数空间分析结果
结合正交经验函数对研究区域年降水量进行空间分析,其特征方差向量及三个主要特征向量的分析结果见表1和图1。
表1 研究区域前10特征向量年降水对应的方差
| 序号 | 特征值 | 差值 | 解释方差比例 | 累积解释方差比例 |
| 1 | 25.892 | 22.715 | 0.700 | 0.700 |
| 2 | 3.177 | 0.775 | 0.086 | 0.786 |
| 3 | 2.402 | 1.086 | 0.065 | 0.851 |
| 4 | 1.315 | 0.182 | 0.036 | 0.886 |
| 5 | 1.133 | 0.087 | 0.031 | 0.917 |
| 6 | 1.047 | 0.176 | 0.028 | 0.945 |
| 7 | 0.871 | 0.109 | 0.024 | 0.969 |
| 8 | 0.762 | 0.041 | 0.021 | 0.989 |
| 9 | 0.721 | 0.085 | 0.019 | 1.009 |
| 10 | 0.635 | 0.094 | 0.017 | 1.026 |
 |  |  |
| 第一特征向量 | 第二特征向量 | 第三特征向量 |
图1 研究区域年降水量不同特征向量空间分布结果
从表中可以看出,在第四个主成分下其特征值下降较为明显,因此前三个主成分作为其主要分析的特征向量,其三个主成分特征值分别为26.0、3.2、2.4,前三个主成分其特征向量累积贡献方差达到85%,所有选用前三个主要特征向量进行区域年降水量空间分析。从三个特征向量空间分析结果可看出,第一特征向量代表年降水空间变化的一致性,即总体呈现一致偏小,第二特征向量表示其年降水量东南和西北方向空间变化差异,从第二特征向量分析结果可看出,特征向量变化正值出现呈现西北方向,表明区域年降水量空间上呈现东南少,西北多的变化特征。第三个特征向量主要表征为东部和西部降雨的变化情况,从其分布情况可看出,特征向量正值主要出现在西部,因此空间表现为东西相反,东少西多的空间变化,从其空间变幅可分析出,各区域年降水空间均有所递减,递减幅度在3~5mm/a之间,且东南部区域降水递减空间变化及变幅最大,东北部变幅最小。
3.3 春季降水正交经验函数空间分析结果
结合正交经验函数对研究区域春季降水量的空间变化进行分析,其特征向量方差变化及主要特征向量空间分布情况见表2及图2。
表2 研究区域前10特征向量春季降水对应的方差
| 序号 | 特征值 | 差值 | 解释方差比例 | 累积解释方差比例 |
| 1 | 34.4997 | 29.2532 | 0.9325 | 0.5222 |
| 2 | 5.2465 | 2.7480 | 0.1418 | 0.6016 |
| 3 | 2.4985 | 0.6145 | 0.0676 | 0.6394 |
| 4 | 1.8840 | 0.5717 | 0.0509 | 0.6679 |
| 5 | 1.3121 | 0.1654 | 0.0355 | 0.6878 |
| 6 | 1.1467 | 0.1402 | 0.0310 | 0.7052 |
| 7 | 1.0064 | 0.2060 | 0.0273 | 0.7203 |
| 8 | 0.8004 | 0.1640 | 0.0216 | 0.7324 |
| 9 | 0.6364 | 0.0241 | 0.0173 | 0.7421 |
| 10 | 0.6123 | 0.0233 | 0.0165 | 0.7514 |
 |  |  |
| 第一特征向量 | 第二特征向量 | 第三特征向量 |
图2 研究区域春季降水量不同特征向量空间分布结果
和年降水空间变化特征向量方差变化较为一致,前三个特征向量为主要成分,从第四个特征向量开始,其特征值变化较为明显,三个主要成分特征向量其特征值分别为34.5、5.2、2.5,其特征向量的累积方差在52.2%~63.9%之间变化。因此选用前三个主成分特征向量作为其春季降水空间变化的主要向量进行分析。从第一特征向量可以看出,正值向量较多,表明区域春季降水总体呈现减少的空间变化一致性,且东南减少的趋势更为明显。第二特征向量表征为东南和西北相同或相反的表征,从图中可看出,负值向量变化较多,表明东南和西北两个方向降水量变化具有相反特征,第三特征向量主要表征为东部和西部春季降水量空间变化的表征,从分析结果可看出,其负值出现出现在东部区域,表明东部春季降水总体减少,而西部春季降水减少趋势较为不明显,从空间降水变幅可分析出,春季降水空间变异度较小,东南区域递减幅度最大,达1.3mm/a,北部降幅为0.8mm/a。
3.4 夏季降水正交经验函数空间分析结果
结合正交经验函数对研究区域夏季降水量的空间变化进行分析,其特征向量方差变化及主要特征向量空间分布情况见表3及图3。
表3 研究区域前10特征向量夏季降水对应的方差
| 序号 | 特征值 | 差值 | 解释方差比例 | 累积解释方差比例 |
| 1 | 28.5800 | 24.4410 | 0.7725 | 0.7725 |
| 2 | 4.1390 | 1.0869 | 0.1118 | 0.8843 |
| 3 | 3.0521 | 1.2606 | 0.0825 | 0.8942 |
| 4 | 1.7915 | 0.2878 | 0.0484 | 0.9143 |
| 5 | 1.5036 | 0.2892 | 0.0407 | 0.9235 |
| 6 | 1.2144 | 0.1843 | 0.0329 | 0.9431 |
| 7 | 1.0301 | 0.1609 | 0.0279 | 0.9469 |
| 8 | 0.8692 | 0.1932 | 0.0235 | 0.9562 |
| 9 | 0.6761 | 0.0091 | 0.0182 | 0.9573 |
| 10 | 0.6670 | 0.0500 | 0.0181 | 0.9658 |
 |  |  |
| 第一特征向量 | 第二特征向量 | 第三特征向量 |
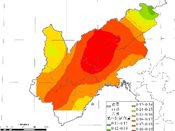
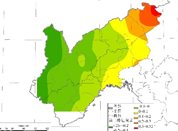
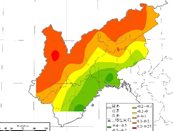
图3 研究区域夏季降水量不同特征向量空间分布结果
从表3中可看出,研究区域夏季降水量也同样表征为前三个特征向量,前三个特征向量的主要累积贡献方差可达到89%,这主要是因为夏季降水量属于区域降水量较为集中的季节,其降水量空间变化特征更为明显。从其三个特征向量空间变化可看出,其夏季降水呈现较为明显的变化一致性,总体呈现减少变化,其中中部降水减少量最明显,正值分布较多,也较为集中。而对于第二特征向量而言,其特征向量的正值均分布在东部区域,表明东部夏季降水变化具有一致性,总体减少,而西北部特征向量分布较少,表明西北部夏季降水量变化较小。第三特征向量主要表征为东部和西部降水空间变化,从第三特征向量分布结果可看出,其在西部的特征向量正值变化较多,西部夏季降水量变化具有一致性,总体减少变化。从其降水空间变幅分析可看出,东南部夏季降水减少幅度均值为2.8mm/a,东北部有所递增,增幅均值达0.7mm/a。
3.5 秋季降水正交经验函数空间分析结果
结合正交经验函数对研究区域秋季降水量的空间变化进行分析,其特征向量方差变化及主要特征向量空间分布情况见表4及图4。
表4研究区域前10特征向量秋季降水对应的方差
| 序号 | 特征值 | 差值 | 解释方差比例 | 累积解释方差比例 |
| 1 | 33.0024 | 27.6039 | 0.8919 | 0.7345 |
| 2 | 5.3985 | 2.9880 | 0.1459 | 0.7651 |
| 3 | 2.4105 | 0.5621 | 0.0651 | 0.7759 |
| 4 | 1.8484 | 0.4129 | 0.0499 | 0.7892 |
| 5 | 1.4356 | 0.2955 | 0.0388 | 0.7963 |
| 6 | 1.1401 | 0.1190 | 0.0308 | 0.8145 |
| 7 | 1.0213 | 0.0501 | 0.0276 | 0.8235 |
| 8 | 0.9712 | 0.1130 | 0.0263 | 0.8354 |
| 9 | 0.8582 | 0.1050 | 0.0232 | 0.8451 |
| 10 | 0.7532 | 0.1667 | 0.0203 | 0.8562 |
 |  |  |
| 第一特征向量 | 第二特征向量 | 第三特征向量 |
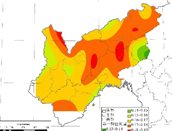
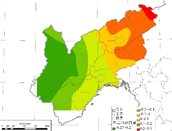
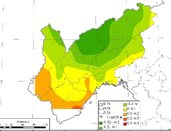
图4 研究区域秋季降水量不同特征向量空间分布结果
秋季降水量总体也表征在前三个主成分的特征向量,前三个特征向量累积方差达到77.6%,从三个特征向量降水空间变化分析结果可看出,第一特征向量下其正值向量总体分布在西部区域,东部区域正值向量分布较少,秋季降水整体空间变化具有一致性。而第二个特征向量表示为东部正值向量较多,西部正值向量分布较少,呈现较为明显的东南和西北降水空间相反变化。从第三个特征向量分布情况可看出,其特征向量正值主要分布在西部,东部降水特征向量正值分布较少,表征出较为明显的东西相反变化。
3.6 冬季降水正交经验函数空间分析结果
结合正交经验函数对研究区域冬季降水量的空间变化进行分析,其特征向量方差变化及主要特征向量空间分布情况见表5及图5。
表5研究区域前10特征向量冬季降水对应的方差
| 序号 | 特征值 | 差值 | 解释方差比例 | 累积解释方差比例 |
| 1 | 35.7968 | 30.4306 | 0.9675 | 0.6659 |
| 2 | 5.3663 | 3.3100 | 0.1451 | 0.6843 |
| 3 | 2.0563 | 0.5742 | 0.0556 | 0.6952 |
| 4 | 1.4822 | 0.3667 | 0.0400 | 0.7235 |
| 5 | 1.1155 | 0.2709 | 0.0302 | 0.7343 |
| 6 | 0.8444 | 0.0396 | 0.0228 | 0.7582 |
| 7 | 0.8050 | 0.1000 | 0.0217 | 0.7653 |
| 8 | 0.7050 | 0.0482 | 0.0190 | 0.7749 |
| 9 | 0.6568 | 0.0571 | 0.0178 | 0.7859 |
| 10 | 0.5997 | 0.2118 | 0.0162 | 0.8143 |
 |  |  |
| 第一特征向量 | 第二特征向量 | 第三特征向量 |
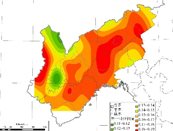
图5 研究区域冬季降水量不同特征向量空间分布结果
区域冬季降水量较少,但其空间变化的整体性和其他季节变化具有相似性,也出现在前三个特征向量上,前三个主成分累积方差的贡献率可以达到69.5%,同样选用三个主成分的特征向量进行其降水空间变化。第一特征向量主要表征其冬季降水空间变化的趋势,从第一特征向量分析结果可看出,其冬季降水空间变化具有较大的差异性,总体变化不具有一致性。第二特征向量主要表征其东南和西北区域降水空间变化,从分析结果可看出,其特征向量正值较少,表现为其东南和西北降水的冬季降水变化具有相反特征。从第三特征向量的分布情况而言,其特征向量分布更少,这主要是冬季降水较少原因所致。从变化结果可看出,区域冬季降水量总体呈现增加变化,西部增加趋势高于东部。从其降水空间变幅可看出,冬季降水有所增加,但增幅较小,东南部有所增加,增幅低于0.2mm/a。
4 结语
各区域年降水空间均有所递减,递减幅度在3~5mm/a之间,且东南部区域降水递减空间变化及变幅最大,东北部变幅最小,应调控降水递减显著区域的水资源配置;
春季降水空间变异度较小,东南区域递减幅度最大,达1.3mm/a,北部降幅为0.8mm/a,春季是区域干旱频发季节,应针对降雨递减明显区域进行抗旱措施规划;
东南部夏季降水减少幅度均值为2.8mm/a,东北部有所递增,增幅均值达0.7mm/a,总体呈现空间相反型变化;
冬季降水有所增加,但增幅较小,东南部有所增加,增幅低于0.2mm/a,东、西部呈现空间相反变化;
本文未能对区域降水空间变化的成因进行分析,在以后研究中还应重点分析其演变的归因。
[2]景淑娟,徐世民.基于M-K方法的大凌河中游降水量时空演变及突变特征分析[J].水利技术监督,2017,25(01):130-133.
[3]杨永利,陈月.基于协同克里金模型的区域降水空间插值方法与应用研究[J].水利技术监督,2016,24(04):104-107.
[4]柴小军,齐广平.张掖市1960—2016年气温和降水特征及突变分析[J].水利规划与设计,2019(01):40-45.
[5]杨海泉.西大河降水时间变化特征与规律分析[J].水利规划与设计,2018(04):36-38.
[6]春兰.内蒙古极端降水指数时空变化及对植被的影响分析[D].内蒙古师范大学,2019.
[7]梅静,王建,何亮,张梦媛,张志刚.川西甘孜州1961—2015年气温和降水时空变化特征研究[J].山地学报,2019,37(02):161-172.
[8]朱艳欣,桑燕芳.青藏高原降水季节分配的空间变化特征[J].地理科学进展,2018,37(11):1533-1544.
[9]陈浩.基于GIS和地统计学的衡水市降水量空间变异性分析[J].水利科技与经济,2018,24(11):52-55.
[10]苟杨,向燕,张伦雨.黔南州近7年3~10月短时强降水时空特征分析[J].吉林农业,2018(21):116.
[11]申莉莉,张迎新,隆璘雪,孙云,康增妹.1981—2016年京津冀地区极端降水特征研究[J].暴雨灾害,2018,37(05):428-434.
[12]张鑫,宋丽萍,王一达.哈尔滨市2014-2017年小时降水特征分析[J].气象灾害防御,2018,25(03):6-9.
[13]冯志刚,陈星,程兴无,徐胜,梁树献.显著经验正交函数分析及其在淮河流域暴雨研究中的应用[J].气象学报,2014,72(06):1245-1256.
[14]孙占东,黄群,姜加虎,OPP Christian.经验正交函数方法和TRMM数据对长江流域降水模式与极端水文过程的研究[J].长江流域资源与环境,2012,21(03):321-326.
[15]游泳,周毅,杨小怡,范伶俐.利用经验正交函数方法(EOF)浅析中国夏季降水时空分布特征[J].四川气象,2003(03):22-23.
