(云南省水文水资源局昆明 650118)
摘要:过去100多年应用和研究的实践证明,糙率很难确定,至今也见不到准确定量的希望。不能苛求于古人,也不能守古而不变。
关键词:均匀流;流速V;水深h;比降i;糙率n
曼宁公式因其形式简单,方便计算和调整,已被广泛使用。结果准确与否完全决定于糙率的取用。凭个人经验或按糙率表取用是常用途径,但与实际多有出入,严重者会埋下祸根,正确的不会是全部。最棘手的是确定历史最高洪水位和比降河段的糙率,没有参考,又不能重演。曾出现过将历史洪水位的糙率定得过大,设计洪水严重偏小,导致工程失事,多少人为之丧命。这都是没有精准的糙率定标准带来的问题。
再看曼宁公式本身:糙率n既作为水流能消耗因素专列式中,为何与河段长度无关呢?断面平均流速决定于n、R、i ,而i的功能已包含了n的全部(附图),为何又要在公式中重复安排n呢?n在算式中能管用。
水文站实测的n~i关系都如图所示,没有例外。可见n的变幅太小,一般0.011~0.060,而i的变幅则很大,两者的相关系数多在0.85以上,i不仅表示水流能耗,还能表示水流原动力的大小(无i水不流),不仅如此,无论河渠壁面多粗糙,多光滑,i都能准确反映出来。这是n无法办到的。
现在资料多了,无需糙率也能求得断面平均流速计算公式
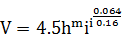
。式中:h≥

时,
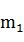
=0.4657;h<

时,
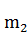
=0.7812。均匀流大小河渠一式通用,准确率还好。但必须i、h准确无误;还要i>2×
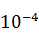
和h>
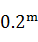
;h>
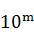
时慎用。
如有特殊需要,还可用另外的算式计算垂线平均流速和断面上任何一点的流速。
实例1:1966年8月,昆明市小河水文站一次实测流量数据如下:施测号数140,断面面积A=29.3

,水面宽度B=15.8m,平均水深h=29.3÷15.8=1.85m,水面比降i=14.6×
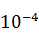
,平均流速V=1.85m/s。试用这些数据验证实测流速。
解:先将比降化为小数i=14.6÷10000=0.00146;

=

=0.18192;

=
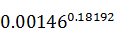
=0.30489;
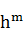
=

=1.332;V=4.5×1.332×0.30489=1.83 m/s。
比实测值1.85 m/s,小0.02 m/s,占比1.1%。证完。
注意:平均水深h一定要使用A÷B,不能使用实测水深的平均值;i,h值一定要测准。
实例2:滇池海口(大烟囱)水文站1965年,施测号数160,实测数据如下:i=2×
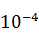
,h=2.21m,V=0.774 m/s,试验证之。
解:V=4.5×
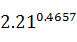
×
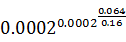
=0.774 m/s。与实测值全等。
实例3:有一2.5m宽的小水渠,实测h=0.75m。水准仪实测高差0.038m,钢尺量距得30m,实测平均流速V=1.04 m/s、试验证之。
计算流速与实测全等。
参考文献:
[1]水利部水司,水文测验手册(第一册附录1-5)河槽糙率系数表,水利出版社,1980年7月
[2]明渠水力学,吴持恭,龙门联合书局,1951年出版
作者简介:徐才俊,(1931年-),男,四川简阳县人,教授级高工,主要从事水文预报、水资源调查评价工作。
田静维,(1986年-),女,云南昆明人,工程师,主要从事水情工作。
